高度に抽象化された現代数学は、さらなる抽象化と同時に私たちの身近に新しい題材を求めています。数学プログラムでは数理解析と情報数理の2大分野によってこの動向に思い切った対処の仕方をしています。数理解析分野では純粋数学の立場からきめ細かな教育・研究を行い、情報数理分野では時代のニーズに応えて情報科学に関する教育・研究を数学の立場から行っています。数学プログラムで私たちと一緒に学んでみませんか？

カリキュラム

授業では、２年次以降、純粋数学の3つの柱でもある代数(数と式)・幾何(図形)・解析（微分や積分）を中心に学びます。

純粋数学の3つの柱を学んだ後、3、４年次では数学特別演習や卒業研究と高度な数学を学ぶ授業/研究へと進みます。数学特別演習や卒業研究では自分自身でテーマを設定し、数学のみならず理学全体の背景を理解します。発表を通じて他者と内容を共有・検討することで、自分自身の考えが論理的に正しく整理されていくプロセスを体感できることでしょう。

本プログラムでは、カリキュラムを学ぶことによって、専門的な知識を活かした職業（教育系、金融、官公庁、IT系）に就くことができます。企業で数学が必要なの？と思う方もいるかもしれませんが、現在いくつもの企業から幅広い知識を持った人材が求められています。数学は具体と抽象を横断的に学ぶ学問であり、「問題をどのように解いたらよいか」ということは数学のみならず企業でも求められていることなのです。

研究紹介

数学プログラムで体系的に学んでいくとみえてくるトピックスをいくつか紹介しておきましょう。

２次方程式の解の公式は習いましたよね？実は3次方程式、4次方程式までは代数的な解の公式が存在します。ところが、一般の5次以上の方程式には、代数的な解の公式が存在しないことが知られています。「代数的な解の公式」「存在しないことが分かる」とはどういうことでしょうか？これは代数学のガロア理論を学ぶことでわかります。また、右の図は正二十面体ですが、この幾何学的な対称性が代数学を用いて説明できます。数と式に関する代数学の概念が、図形の分類につながっているのは不思議な気がしませんか？

式を見てください。上側は1=1/1+1/3-1/2+…であり、下側は2=1/1+1/3+1/5+…となっていますね。実はそれぞれ右辺に登場する数は同じで、順番だけを変えたものです。ところが、収束する値は異なるという奇妙なことが起こります。さらに、右辺の項を並べ替えることで、任意の値に収束させることもできます。皆さんが高校数学で感じている収束のイメージとはかなり違うのではないでしょうか？この理由を深く学ぶこともできます。

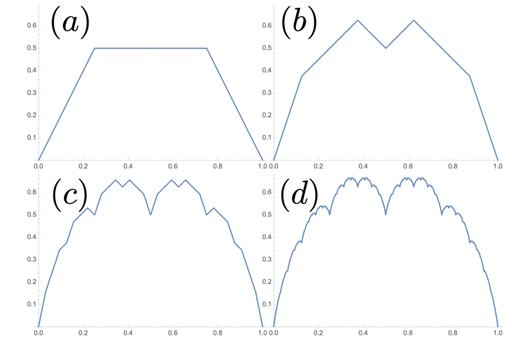
図(d)は高木曲線と呼ばれる関数のグラフです。この関数は、図(a) 、(b) 、(c) 、(d)のようにある操作を無限回繰り返すことで定まります。この関数にはいくつか面白い特徴があります。まずこの関数はどの点でも連続ですが、どの点でも微分不可能であることが知られています。次に曲線の長さに対応するものは無限大となります。ところが、囲まれる面積(曲線とx=0とx=1とy=0で囲まれる青い領域)は有限となります。これらの特徴は皆さんよく知る関数のイメージとは違うのではないでしょうか？このような関数を研究するには、大学で学ぶ「厳密な」解析学が必要です。

TOPICS

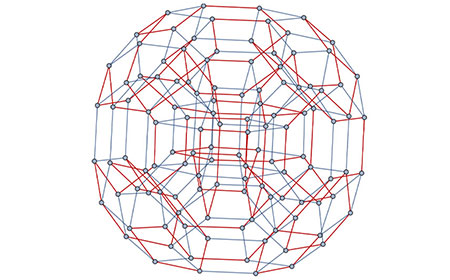
ハミルトン閉路の初等的な求め方

教授　山根 宏之

初めに：　筆者は、１９９０年代に$A − G $型の有限次元複素単純リー超代数の定義関係式を求めました$[1], [2], [3]$。リー超代数の研究には、対称群、ワイル群およびコクセター群の一般化であるワイル亜群が表れます。

Read More

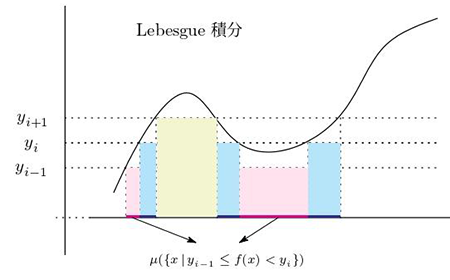
積分を特徴付ける3つの性質　
‐測度を定める汎関数‐

教授　菊池 万里

「（定）積分」と聞いて先ず（というより唯一）思い浮かぶのは、高校で学習した\[ \int_a^b f(x)\,dx \]という形の積分だと思います。

Read More

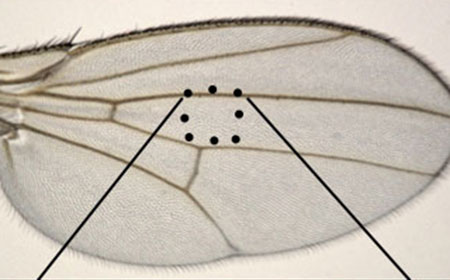
現象解明に数学は使える！

准教授　秋山 正和

2021年11月1日より理学部数学科に着任しました秋山正和と申します．今回は，数学が現象の解明に役立つ可能性を秘めているものであるということをお話させて頂きます．

Read More

教員と研究テーマ