積分を特徴付ける3つの性質　‐測度を定める汎関数‐

【数学科】菊池 万里

　「（定）積分」と聞いて先ず（というより唯一）思い浮かぶのは、高校で学習した \[ \int_a^b f(x)\,dx \] という形の積分だと思います。このような積分をリーマン積分と呼びます。リーマン積分は連続でない関数に対しても定義されますが、 高校では連続関数のみを積分の対象としています。
　リーマン積分は、スティルチェス積分と呼ばれる積分に一般化されます。詳しいことは省略しますが、 $g(x)$が区間$[a,b]$上の単調増加な（すなわち $x< y$であれば $g(x)\leqq g(y)$となるような）関数であれば、 \[ \int_a^b f(x)\,dg(x) \] という形の積分が定義できます。 $g(x)=x$の場合が高校で学習するリーマン積分です。 勿論もちろん、$g(x)$によって積分の値が変化します。 例えば、区間$[0, \pi/4]$上の関数$g(x)$を$g(x)=x^2$のように定義すれば，$g(x)$はこの区間で単調増加であり、 \[ \int_0^{\pi/4} \sin x\,dg(x) =\int_0^{\pi/4} \sin x\,dx^2=\sqrt{2}-\frac{\pi}{2\sqrt{2}} \] となります。

　このように、高校で学習したものだけではなく、様々な積分が存在します。 とはいえ、同じ「積分」という言葉で表されるものであるからには、様々な積分に「共通の何か」があるはずです。 その「共通の何か」とはどのようなものでしょうか。 この問いに答えるために、先ず、「積分とは1つの実数値関数に対して1つの実数を対応させる決まりである」 ということを認識する必要があります^*1。 このように1つのものに対して1つのものを対応させる決まり（規則）のことを写像と呼びます。 結論を急げば、以下に述べる本稿の主定理の通り、積分とはある種の条件を満たす写像のことです。 その定理を紹介するための準備として、必要となる概念や記号の導入から始めます。
　$\mathfrak E$（ドイツ文字のE）を集合$X$で定義された実数値関数の集合で、次の条件を満たすものとします （従って$\mathfrak E$の要素は$X$上の実数値関数です）。

• $f(x),\;g(x)\in {\mathfrak E}$であれば、任意の実数$a,\;b$に対して$af(x)+bg(x)\in {\mathfrak E}$
• $f(x),\;g(x)\in {\mathfrak E}$であれば、$f(x)\vee g(x)\in {\mathfrak E}$かつ$f(x)\wedge g(x)\in {\mathfrak E}$
• $f(x)\in {\mathfrak E}$であれば、$f(x)\wedge 1\in {\mathfrak E}$

但し、2つの関数$f(x),\;g(x)$に対し、 \[ f(x)\vee g(x)=\max\{f(x),\;g(x)\},\qquad \quad f(x)\wedge g(x)=\min\{f(x),\;g(x)\} \] とします。すなわち、$f(x)\vee g(x)$は$x$に対し、$f(x)$と$g(x)$の大きい方の数を対応させる関数であり、 $f(x)\wedge g(x)$は$x$に対し、$f(x)$と$g(x)$の小さい方の数を対応させる関数です。 文献 [1] に従って、上記の条件を満たす関数の集合を$X$上の初等関数族と呼ぶことにします。

　集合$X$上の実数値関数の列$f^{}_1(x),\;f^{}_2(x),\ldots,f^{}_n(x),\ldots$が、各点$x$で$n$に関して増加しながらある$X$上の関数$f(x)$に収束するとき、 $f^{}_n(x)\uparrow f(x)$と書き、$f^{}_1(x),\;f^{}_2(x),\ldots,f^{}_n(x),\ldots$が、各点$x$で$n$に関して減少しながら$f(x)$に収束するとき、 $f^{}_n(x)\downarrow f(x)$と書くことにします。すなわち、

• - $f^{}_n(x)\uparrow f(x)$とは、各点$x$において$f^{}_n(x) \leqq f^{}_{n+1}(x)$ かつ $f(x)=\lim\limits_{n\to \infty}f^{}_n(x)$となること
• - $f^{}_n(x)\downarrow f(x)$とは、各点$x$において$f^{}_n(x) \geqq f^{}_{n+1}(x)$ かつ $f(x)=\lim\limits_{n\to \infty}f^{}_n(x)$となること

ということです。このような記法の下に、次の定理が成立します。

　この定理の証明は、文献 [1] に付録として記載されています。
　上記の定理において「測度」という聞きなれない言葉が出てきました。 これは、高校で学習するリーマン積分の拡張であるルベーグ積分^*2の理論を展開する際に利用される数学的概念です。 従って定理の中に出てくる積分は、ルベーグ積分です。

　高校で学習する「連続関数に関するリーマン積分」は、微分積分学の基本定理と呼ばれる定理を介して、 微分の逆演算と解釈でき、（分かり易いか否かは別として）高校の範囲で学習可能であるという利点があります。 一方で、リーマン積分は極限操作に弱く、$\lim\limits_{n\to \infty}f^{}_n(x)=f(x)$であるような関数の列 $f^{}_1(x),\;f^{}_2(x),\; f^{}_3(x),\ldots$に対して、かなり強い条件を課さない限り \[ \lim_{n\to \infty}\int_a^b f^{}_n(x)\,dx=\int_a^b f(x)\,dx \] のような基本的な等式が得られません。この弱点を克服すべく、ジョルダンやボレルなど、優秀な多くの数学者が考察を重ね、 最終的にフランスの数学者アンリ・レオン・ルベーグが新たな積分論を築き上げました （上記の定理の積分$\int_X f(x)\,\mu(dx)$がどのように定義されるかについて、興味があれば下記の付録をご覧ください）。

　実際、ルベーグ積分では、リーマン積分の極限操作に関する弱点が「克服」されています。 例えば、$\nu$を集合$X$上の測度とするとき、（$\nu$に関して積分可能で）$f^{}_n(x)\downarrow 0$であるような関数列に対しては、 \[ \lim_{n\to \infty}\int_X f^{}_n(x)\,\nu(dx)=\int_X 0\,\nu(dx)=0 \] となることが、優収束定理と呼ばれる定理から導かれます。また、各点$x$において$f(x)\geqq 0$であれば \[ \int_X f(x)\,\nu(dx)\geqq 0 \] となること、及び、 \[ \int_X \bigl\{f(x)+g(x)\big\}\,\nu(dx) =\int_X f(x)\,\nu(dx)+\int_X g(x)\,\nu(dx) \] であることもルベーグ積分の基本的な性質として成立します。この事実は、「定理の条件(T1)$,$ (T2)$,$ (T3)は、写像$T$が定理のように積分で表されることの必要十分条件である」ということを意味します。 少々乱暴な言い方になるかもしれませんが、この事実を端的に表現すれば、

ということになります。この事実をそのまま受け止めれば、大学での積分論の講義も、 「ルベーグ積分とは(T1)$,$ (T2)$,$ (T3)を満たす写像のことである」というだけで終わりではないか、 という疑問が生まれますが、そういう訳にはいかないのが現実です。これだけでは積分論の本質を理解したとは言えないし、 実際の計算ができないのも事実です。

参考文献

• [1] 伊藤 清, 確率論, 岩波基礎数学選書, 岩波書店

---

^*1 高校で学習する積分を例に取れば、区間$[a,b]$を固定するとき、 1つの関数$f(x)$に対して定積分$\int_a^b f(x)\,dx$という1つの実数が対応しています。

^*2 ルベーグ積分という言葉を狭い意味で使用する場合には、 ユークリッド空間$\mathbb R^n$上のルベーグ測度に関する積分を指しますが、 広い意味では抽象的な測度空間における積分を指すこともあります。本稿では後者の立場を取ります。

付録
　理学部数学科の学生に向けて開講される数学の講義の中で、分り難いものの1つが積分論 （富山大学の講義名では実解析学Ⅰ、及び、実解析学Ⅱ）です。 積分論とは、高校で学習するリーマン積分を拡張するルベーグ積分に関する理論です。 アンリ・レオン・ルベーグが27歳のときに執筆した学位論文「積分・長さおよび面積（Intégrale, Longueur, Aire）」の中で確立された新しい積分がルベーグ積分です。 以下にルベーグ積分についてその定義の概要を記述します。
　集合に数を対応させる決まりを集合関数と呼びます。例えば、集合$A$に対して、その要素の数$\#(A)$を対応させる決まりは集合関数です。 要するに、集合関数とは「集合を変数とする関数」です。集合関数の定義域は、集合の集合ということになります（集合の集合を集合族と呼びます)。 集合$X$の部分集合$A$に対して、0以上の実数$\mu(A)$を対応させる集合関数が、2条件

• (m1)  $\mu(\varnothing)=0$
• (m2)  異なる$k,\,\ell$に対して$A_k\cap A_{\ell}=\varnothing$であれば、 $\mu\Bigl(\,\bigcup\limits_{k=1}^{\infty}A_k\Bigr)=\sum\limits_{k=1}^{\infty}\mu(A_k)$ ^*3

を満たすとき、$\mu$を$X$上の測そく度どと呼びます。 $\bigcup\limits_{k=1}^{\infty} A_k$は、$A_1,\,A_2,\,A_3,\ldots$のうち、少なくとも1つの$A_n$に属す点$x$の全体からなる集合です。

　例えば、集合$A$に対して \[ \mu(A)=\#(A)=\text{$A$の要素の数} \] と置けば、$\mu$は$X$上の測度になります。 更に、$X=\mathbb R$の場合（$\mathbb R$は実数の全体を表す記号です）には、$X=\mathbb R$上の測度${\mathrm m}$を \begin{equation*} \text{区間$I=[a,b]$に対して${\mathrm m}(I)=b-a$} \tag{$\ast$} \label{eq:ast} \end{equation*} となるように構成することができます。これをルベーグ測度と呼びます。 このルベーグ測度の構成には複雑な手順が必要であり、初学者には容易ではありません。 これが「積分論は難しい」と感じさせる1つの（しかも大きな）要因です。 条件\eqref{eq:ast}から、ルベーグ測度${\mathrm m}$は区間の長さを拡張する集合関数であると解釈できます。 交わらない2つ区間$I=[a,b],\;J=[c,d]$に対して、それらの和集合$I\cup J$のルベーグ測度${\mathrm m}(I\cup J)$は$I$の長さと$J$の長さの和になりますので、 ルベーグ測度が区間の長さの拡張であるという解釈は自然であろうと思います。

　但し、ルベーグ測度の場合は、すべての$\mathbb R$の部分集合$A$に対して${\mathrm m}(A)$が定義されるわけではありません。 イタリアの数学者ヴィタリによって、「すべての$\mathbb R$の部分集合$A$に対して、条件(\ref{eq:ast})を満たすように測度を定めることができない」こと （ルベーグ非可測集合の存在）が証明されました。しかしそれでも、「定義域を性質のよい${\mathbb R}$の部分集合に制限することにより、 条件\eqref{eq:ast}を満たす$\mathbb R$上の測度${\mathrm m}(A)$を構成することができる」ということがルベーグによって証明されました。 この事実こそが、ルベーグによる積分論の核心部分です。

　ルベーグ測度が定義される集合の全体（ルベーグ測度の定義域）を$\mathfrak M$で表すとき、 $\mathfrak M$は次の3条件を満たします。

• ($\sigma$1)  $\mathfrak M$は$\varnothing$を含む
• ($\sigma$2)  $A$が$\mathfrak M$に属せば、$A$の補集合$\{x\in \mathbb R\colon x\notin A\}$も$\mathfrak M$に属す
• ($\sigma$3)  $A_1,\,A_2,\,A_3,\ldots$が$\mathfrak M$に属せば、$\bigcup\limits_{k=1}^{\infty}A_k$も$\mathfrak M$に属す

この3条件を満たす集合族（集合の集合）を$\mathbb R$上の完全加法族、 ${\boldsymbol \sigma}$-加法族、${\boldsymbol \sigma}$-集合体、 ${\boldsymbol \sigma}$-代数などと呼びます。呼び方は様々ですが、 いずれも上記の($\sigma$1)$,$ ($\sigma$2)$,$ ($\sigma$3)を満たす集合族（集合の集合）のことです。

　$X$が一般の集合で、$\mu$が$X$上の測度の場合に戻ります。$\mathfrak F$（ドイツ文字のF）を$X$上の完全加法族とし、 $\mu$を定義域が$\mathfrak F$であるような$X$上の測度とします。換言すれば、$\mathbb R$を$X$で置き換え、 $\mathfrak M$を$\mathfrak F$で置き換えて($\sigma$1)$,$ ($\sigma$2)$,$ ($\sigma$3)が成り立ち、更に(m1)$,$ (m2)が成り立つとします。 $\mathfrak F$に属す集合$A$に対して、関数${\mathbf 1}_A(x)$を \[ {\mathbf 1}_A(x)=\left\{\begin{array}{ll} 1 & (x\in A) \\ 0 &(x\notin A) \end{array}\right. \] のように定義します。すなわち、${\mathbf 1}_A(x)$は$x$が$A$に属していれば1、 属していなければ0という値を取る関数です（関数は定義域の各点に対応する実数さえ明確に決められていれば、数式で表されている必要はありません）。 ${\mathfrak F}$に属す$k$個の集合$A_1,\,A_2,\ldots,A_k$と$k$個の実数$a^{}_1,\,a^{}_2,\ldots,a^{}_k$を用いて \begin{equation*} f(x)=a^{}_1{\mathbf 1}_{A_1}(x)+a^{}_2{\mathbf 1}_{A_2}(x)+\cdots +a^{}_k{\mathbf 1}_{A_k}(x) \tag{$\ast\ast$} \label{eq:astast} \end{equation*} のように表される関数$f(x)$を$\boldsymbol{\mathfrak F}$-可測単関数と呼びます。但し、${\mathfrak F}$-可測単関数ごとに$k$の値は変化します。

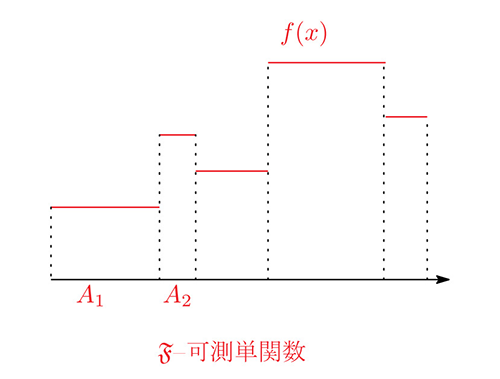
数式\eqref{eq:astast}のように表される${\mathfrak F}$--可測単関数$f(x)$に対して、その$\mu$に関する積分を \[ \int_X f(x)\,\mu(dx) =a^{}_1\,\mu(A_1)+a^{}_2\,\mu(A_2)+\cdots+a^{}_k\,\mu(A_k) \] のように定義します。

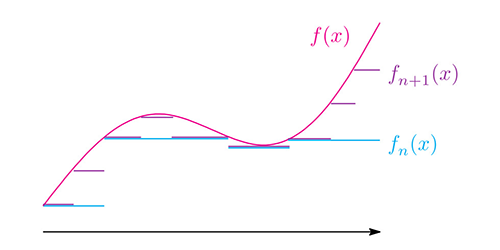
　次に、$f(x)$を$X$の各点で0以上の値を取る関数とします（このような関数を非負関数と呼びます）。 ${\mathfrak F}$-可測単関数の列$f^{}_1(x),\;f^{}_2(x),\;f^{}_3(x),\ldots$をうまく取って$f^{}_n(x) \uparrow f(x)$とできるとき、 $f(x)$を$X$上の非負${\boldsymbol{\mathfrak F}}$-可測関数と呼びます。

　最後に、各点で0以上の値を取るとは限らない$X$上の関数$f(x)$に対して、関数$f^+(x),\;f^-(x)$を \[ f^+(x)=f(x)\vee 0=\max\{f(x),\;0\}, \qquad f^-(x)=(-f(x))\vee 0=\max\{-f(x),\;0\} \] のように定義します。勿論、$f^+(x),\;f^-(x)$は0以上の値を取る関数になります。更に$f(x)=f^+(x)-f^-(x)$となることも容易に確かめられます。

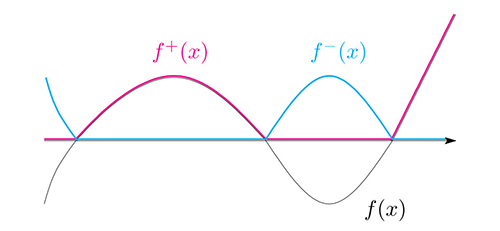
$f^+(x),\;f^-(x)$の双方が非負${\mathfrak F}$-可測関数となるとき、$f(x)$を（単に）${\mathfrak F}$-可測関数と呼びます。 このような関数に対しては、上述のように \[ \int_X f^+(x)\,\mu(dx), \qquad \int_X f^-(x)\,\mu(dx) \] が定義されます。上記の2つの積分のうち、少なくとも一方が有限であるとき（$\pm\infty$でないとき）、$f(x)$の$\mu$に関する積分を \[ \int_X f(x)\,\mu(dx)=\int_X f^+(x)\,\mu(dx)-\int_X f^-(x)\,\mu(x) \] のように定義します。但し、$f^-(x)$の積分が有限で、$f^+(x)$の積分が$+\infty$であるときは、$f(x)$の積分は$+\infty$であると解釈し、 $f^+(x)$の積分が有限で$f^-(x)$の積分が$+\infty$であるときは、$f(x)$の積分は$-\infty$であると解釈します。 $f^+(x),\;f^-(x)$の双方の積分が有限であるとき、$f(x)$は$\mu$に関して積分可能である、或いは、可積分であるといいます。

　このように定義した積分に対して、 \[ T(f)=\int_X f(x)\,\mu(dx) \] と置くと、$T(f)$は本稿主定理の(T1)$,$ (T2)$,$ (T3)を満たし、逆に、(T1)$,$ (T2)$,$ (T3)を満たす$T(f)$はある測度$\mu$を用いて、 上記のように表されるということになります。

---

^*3(m2)の等式は、両辺が$+\infty$になっても構いません。