研究トピックス TOPICS
- ホーム
- 研究トピックス一覧
- 数学科の研究トピックス一覧
- 研究トピックス
ハミルトン閉路の初等的な求め方
【数学プログラム】山根 宏之
初めに: 筆者は、1990年代に$A − G $型の有限次元複素単純リー超代数の定義関係式を求めました$[1], [2], [3]$。リー超代数の研究には、対称群、ワイル群およびコクセター群の一般化であるワイル亜群が表れます。筆者は、共同研究でワイル亜群の本質的な結果を得ました$[4]$。これらの論文は今でも他の研究者の論文で引用され続けています。最近はワイル亜群のケイリーグラフのハミルトン閉路の研究をしています$[6], [7]$。この論説ではグラフのハミルトン閉路の初等的な求め方である定理A と定理B を解説します。ただし、任意のグラフにハミルトン閉路が存在するとは限りません。また存在しても必ずしも定理A や定理B のアイデアで求まるわけではありません。
集合: ものの集まりを集合と言います。ものは要素と呼ばれたり、元と呼ばれたりします。$A$ を集合とします。$a$ が$A$ の元であるとき$a ∈ A $と書き、そうでないときは、$a \notin A $と書きます。元のない集合を空集合と言い$∅$ で表します。集合$B$ が$A$ の部分集合であるとは「$b ∈ B$ ならば$b ∈ A$」を意味し、$B ⊂ A$ と書きます。$∅$ は$A$の部分集合であり、$∅$ $⊂ A$と書いて構いません。$P(A)$ を$A$の部分集合を元とする集合とします。$P(A)$ を$A$ のべき集合と言います。この論説のみの記号として2つの元の部分集合を元とする集合を$P_2(A)$ と書きます。$P_2(A) ⊂ P(A)$
です。$A$ の元の個数を$n(A)$ で表します。
例えば$A$ が{$1, 2, 3$} であるときは、$n(A)$ = $n$({$1, 2, 3$}) = $3$ であり、
\[ P(A) = P(\{1, 2, 3\}) = \{∅, \{1\}, \{2\}, \{3\}, \{1, 2\}, \{1, 3\}, \{2, 3\}, \{1, 2, 3\}\}
\]
です。$P_2(A) = \{\{1, 2\}, \{1, 3\}, \{2, 3\}\}$ です。
写像: 集合$A$から集合$B$ への対応を写像と言い$f : A → B$ と書きます。$a ∈ A$に対して$f(a) ∈ B$ が対応します。例えば、$\{1, 2\}$ から$\{1, 2, 3\}$ への写像は次の9個の写像$g_i : \{1, 2\} → \{1, 2, 3\} (1 ≦ i ≦ 9)$ です。
- $g_1(1) = 1,g_1(2) = 1, g_2(1) = 1, g_2(2) = 2, g_3(1) = 1,g_3(2) = 3,$
- $g_4(1) = 2, g_4(2) = 1, g_5(1) = 2, g_5(2) = 2, g_6(1) = 2, g_6(2) = 3,$
- $g_7(1) = 3, g_7(2) = 1, g_8(1) = 3, g_8(2) = 2, g_9(1) = 3, g_9(2) = 3$
- $h_1(1) = 1, h_1(2) = 1, h_1(3) = 1, h_2(1) = 1, h_2(2) = 1, h_2(3) = 2,$
- $h_3(1) = 1, h_3(2) = 2, h_3(3) = 1, h_4(1) = 1, h_4(2) = 2, h_4(3) = 2,$
- $h_5(1) = 2, h_5(2) = 1, h_5(3) = 1, h_6(1) = 2, h_6(2) = 1, h_6(3) = 2,$
- $h_7(1) = 2, h_7(2) = 2, h_7(3) = 1, h_8(1) = 2, h_8(2) = 2, h_8(3) = 2$
$f : A → B$ を写像とします。条件「$a\ne {{a^\prime}}$ならば$f(a)\ne f({{a^\prime}})$」をみたすとき$f$は単射であると言います。上の例で単射なものは$g_2, g_3, g_4, g_6, g_7, g_8$ です。また、条件「各$b ∈ B$ に対して$f(a) = b$ となる$a ∈ A$が必ずとれる」をみたすとき$f$ は全射であると言います。上の例で全射なものは$h_2, h_3, h_4, h_5, h_6, h_7$ です。$f$ が単射かつ全射であるとき、$f$ は全単射であると言います。$\{1, 2, 3\}$ から$\{1, 2, 3\}$ への全単射である写像は次の6個の写像$k_r : \{1, 2, 3\} → \{1, 2, 3\} (1 ≦ r ≦ 6)$ です。
- $k_1(1) = 1, k_1(2) = 2, k_1(3) = 3, k_2(1) = 1, k_2(2) = 3, k_2(3) = 2,$
- $k_3(1) = 2, k_3(2) = 1, k_3(3) = 3, k_4(1) = 2, k_4(2) = 3, k_4(3) = 1,$
- $k_5(1) = 3, k_5(2) = 1, k_5(3) = 2, k_6(1) = 3, k_6(2) = 2, k_6(3) = 1$
写像の合成: 写像 $f : A → B, g : B → C$ に対して写像 $g \circ f : A → C $ を$(g \circ f)(a) = g(f(a)) (a ∈ A) $ により定義します。 $g \circ f$ を合成写像と言います。写像$f : A → B, g : B → C, h : C → D,$ に対して \[h \circ (g \circ f) = (h \circ g) \circ f \] が成り立ちます。
自然数全体の集合を $\mathbb{N}$ で表します。すなわち、 \[\mathbb{N} = \{1, 2, 3, . . .\} \] です。
グラフ: $V$ を空ではない集合とします。$E$ を $P_2(V )$ の部分集合とします。$E ⊂P_2(V )$ です。グラフの数学としての定義は、組 $(V,E)$ です。 $v ∈ V$ に対して$D(v) :=\{w ∈ V |\{v,w\} ∈ E\}$ とおきます。$D(v)$ の元の個数$n(D(v))$ を$d(v)$ で表します。
$V$ の元を「頂点」と呼びます。$E$ の元を「辺」と呼びます。
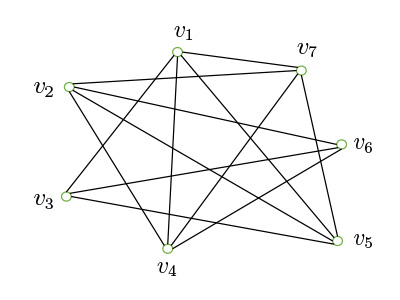
例として$(V,E)$ を下記の図1の表わすグラフとすると、次の通りです。 \begin{equation*}\begin{array}{l} V=\{v_1,v_2,v_3,v_4,v_5,v_6,v_7\}, \\E=\{\{v_1,v_3\}, \{v_1,v_4\}, \{v_1,v_5\}, \{v_1,v_7\}, \{v_2,v_4\}, \{v_2,v_5\}, \{v_2,v_6\}, \{v_2,v_7\}, \\ \quad \quad \,\, \{v_3,v_5\}, \{v_3,v_6\}, \{v_4,v_6\}, \{v_4,v_7\}, \{v_5,v_7\} \}, \\d(v_1)=d(v_2)=d(v_4)=d(v_5)=d(v_7)=4,\,\,d(v_3)=d(v_6)=3 \end{array} \end{equation*}
ハミルトン閉路: $n\in\mathbb{N}$を$n\geqq 3$であるものとします。$(V,E)$を$n=n(V)$をみたすグラフとします。すなわち集合$V$の元の個数は$n$です。(この$n$と$n(V)$の$n$無関係です。) 全単射な写像$f:\{1,2,\ldots,n\}\to V$がハミルトン閉路であるとは、 \[ \{f(i),f(i+1)\}\in E\,\,(1\leqq i\leqq n-1)\quad \mbox{および} \quad\{f(n),f(1)\}\in E \]をみたすときに言います。 ハミルトン閉路が存在するとき$(V,E)$をハミルトン閉路グラフと言います。$3\leqq m\leqq n$とします。単射な写像$g:\{1,2,\ldots,m\}\to V$が閉路であるとは、$\{g(i),g(i+1)\}\in E$ $(1\leqq i\leqq m-1)$ および$\{g(m),g(1)\}\in E$をみたすときに言います。
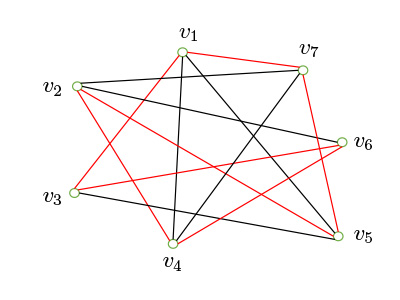
下記の図1の表すグラフのハミルトン閉路は図2の赤い辺の部分です。
定理A(オーレの定理): $n\in\mathbb{N}$を$n\geqq 3$であるものとする。グラフ$(V,E)$が$n=n(V)$および次の条件$(*)$をみたすとする。
(*) $\quad\quad \{v,w\}\in P_2(V)$が$\{v,w\}\notin E$であるならば$d(v)+d(w)\geqq n$
このとき$(V,E)$はハミルトン閉路グラフである。
証明: ([8] を参考にした。) $n=3$のときは簡単であるので$n \geqq 4$と仮定する。
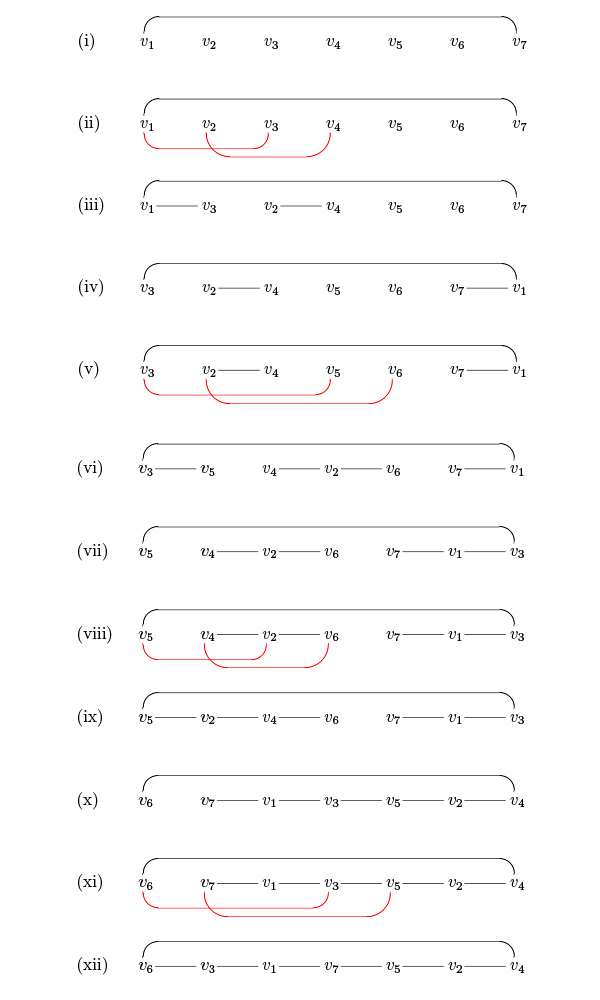
$V=\{v_1,v_2,\ldots,v_n\}$とする。以下の手順を繰り返すことによりハミルトン閉路である全単射な写像$f:\{1,2,\ldots,n\}\to V$を得ることができる。
$\{v_i,v_{i+1}\}\in E$ $(1 \leqq i\leqq n-1)$および$\{v_n,v_1\}\in E$であるならばハミルトン閉路$f$を$f(i)=v_i$ $(1\leqq i\leqq n)$により定義すればよい。そうでなければつぎの(あ)、(い)または(う)の状態である。
- (あ) $\{v_1,v_2\}\notin E$である。
- (い) $\{v_i,v_{i+1}\}\notin E$である$2\leqq i\leqq n-1$が存在する。
- (う) $\{v_n,v_1\}\notin E$である。
(あ)であるならば$v_1,v_2,\ldots,v_n$をそのままにする。
(い)であるならば$v_1,v_2,\ldots,v_n$の順序を、 \begin{equation*} \left\{\begin{array}{l} \mbox{$v_i ,v_{i+1},\ldots,v_n$をそれぞれ新しい$v_1 ,v_2,\ldots,v_{n-i+1}$にして、} \\ \mbox{$v_1,v_2,\ldots,v_{i-1}$をそれぞれ新しい$v_{n-i+2},v_{n-i+3},\ldots,v_n$に} \end{array}\right. \end{equation*} することにより定義する。
(う)であるならば$v_1,v_2,\ldots,v_n$の順序を、 \begin{equation*} \left\{\begin{array}{l} \mbox{$v_n$を新しい$v_1$にして、} \\ \mbox{$v_1,v_2,\ldots,v_{n-1}$をそれぞれ新しい$v_2,v_3,\ldots,v_n$に} \end{array}\right. \end{equation*} することにより定義する。
新しい$v_1,v_2,\ldots,v_n$に対して$\{v_1,v_2\}\notin E$である。 \begin{equation*} \begin{array}{lcl} A & = & \{i\in\{1,2,\ldots,n\}|3\leqq i\leqq n, \{v_1,v_i\}\in E\}, \\ B & = & \{i\in\{1,2,\ldots,n\}|3\leqq i\leqq n, \{v_2,v_i\}\in E\} \end{array} \end{equation*}とおく。$(*)$より$n(A)+n(B)\geqq n$が成り立つ。 \begin{equation*} C=\{i\in\{1,2,\ldots,n\}|3\leqq i\leqq n-1, i\in A, i+1\in B\} \end{equation*}とおく。
$(\sharp)$ $C$は空集合ではない。すなわち、$C\ne\emptyset$, $n(C)\geqq 1$である。
($(\sharp)$の証明: $A^\prime=\{i\in\{1,2,\ldots,n\}|3\leqq i\leqq n-1, i\in A \}$とおく。 $n\notin A$のとき$A^\prime=A$である。 $n\in A$のとき$A=A^\prime\cup\{n\}$であるので$n(A^\prime)=n(A)-1$である。 $B^\prime:=\{i\in\{1,2,\ldots,n\}|3\leqq i\leqq n-1, i+1\in B\}$とおく。 $C=A^\prime\cap B^\prime$である。 $3\notin B$のとき、$n(B^\prime)=n(B)$であり、$3\in B$のとき、$n(B^\prime)=n(B)-1$である。 次の等式が成り立つ。 \begin{equation*} \begin{array}{l} n(\{i\in\{3,\ldots,n-1\}|i\notin B^\prime\} )\\ \quad = (n-3)-n(B^\prime) \\ \quad = \left\{\begin{array}{ll} (n-3)-n(B) & (\mbox{$3\notin B$のとき}), \\ (n-3)-(n(B)-1) & (\mbox{$3\in B$のとき}), \end{array}\right. \\ \quad \leqq (n-2)-n(B) \\ \quad \leqq n(A)-2 \\ \quad < n(A)-1 \\ \quad \leqq n(A^\prime) \end{array} \end{equation*} よって、$A^\prime\cap B^\prime\ne\emptyset$である。 ゆえに$C\ne\emptyset$である。 $(\sharp)$の証明終わり。)
$i\in C$とする。$v^\prime_j\in V$ $(1\leqq j\leqq n)$を次で定義する。
\begin{equation*} v^\prime_j =\left\{ \begin{array}{ll} v_1 & \quad (\mbox{$j=1$のとき}), \\ v_{i-j+2} & \quad (\mbox{$2\leqq j\leqq i$のとき}), \\ v_j & \quad (\mbox{$i+1\leqq j\leqq n$のとき}) \end{array}\right. \end{equation*} $P_2(V)$の部分集合$H$, $H^\prime$を、それぞれ、 \begin{equation*} \begin{array}{lcl} H &:= & (\{\{v_k,v_{k+1}\}|1\leqq k\leqq n-1\}\cup\{\{v_n,v_1\}\})\cap E, \\ H^\prime &:= & (\{\{v^\prime_k,v^\prime_{k+1}\}|1\leqq k\leqq n-1\}\cup\{\{v^\prime_n,v^\prime_1\}\} )\cap E \end{array} \end{equation*} により定める。 つぎの等式を得る。 \begin{equation*} \begin{array}{lcl} n(H^\prime) & = & \left\{\begin{array}{ll} n(H)+2 & \quad\mbox{$\{v_i,v_{i+1}\}\notin E$のとき}, \\ n(H)+1 & \quad\mbox{$\{v_i,v_{i+1}\}\in E$のとき}, \end{array}\right. \\ & > & n(H) \end{array} \end{equation*} $v^\prime_1,\ldots, v^\prime_n$を、 新たな $v_1,\ldots, v_n$としてこの手順を繰り返せばよい。 $\Box$
下記の図1の表わすグラフに上の定理の証明を適用すると、下記の手順(i)~(xii)で図2の赤い辺の部分が表すハミルトン閉路が得られます。
対称群: $n\in\mathbb{N}$とします。
$S_n$を$\{1,2,\ldots,n\}$から$\{1,2,\ldots,n\}$への全単射な写像全体の集合とします。$S_n$を$n$次対称群と言います。$n=3$のとき$k_1,\ldots,k_6$を上のものとすると、$S_3=\{k_1,k_2,k_3,k_4,k_5,k_6\}$です。$1\leqq i\leqq n-1$に対して$s_i\in S_n$を以下で定義します。
\begin{equation*}
s_i(j)=
\left\{\begin{array}{ll}
i+1 & \quad\mbox{($j=i$のとき)}, \\
i & \quad\mbox{($j=i+1$のとき)}, \\
j & \quad\mbox{($j\ne i, i+1$のとき)}
\end{array}\right.
\end{equation*}
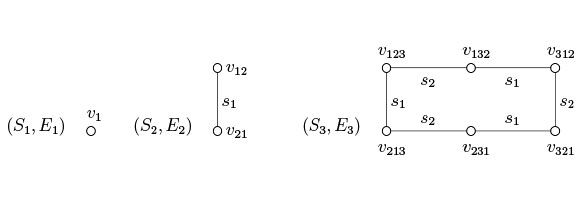
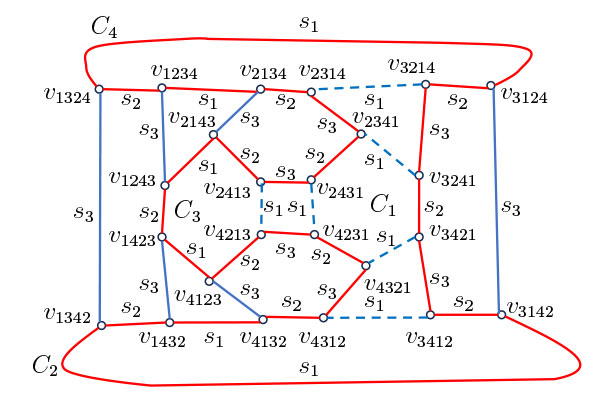
$s_i$を基本互換と言います。$(w\circ s_i)\circ s_i=w$ $(w\in S_n, 1\leqq i\leqq n-1\})$が成り立ちます。$S_n$の部分集合$X_n$を、$X_n=\{s_i|1\leqq i\leqq n-1\}$により定めます。$n=1$のとき$X_1=\emptyset$です。$P_2(S_n)$の部分集合$E_n$を、$E_n=\{\{w,w\circ s_i\}|w\in S_n,1\leqq i\leqq n-1\}$により定めます。グラフ$(S_n,E_n)$を、$S_n$の$X_n$によるケイリーグラフと言います。$w\in S_n$を$v_{w(1)w(2)\cdots w(n)}$により表します。$n=1,2,3$のときは以下の通りです。(図3も見て下さい。)\begin{equation*}
\begin{array}{l}
S_1=\{v_1\}, E_1=\emptyset,\quad S_2=\{v_{12}, v_{21}=s_1\}, E_2=\{\{v_{12},v_{21}\}\}, \\
S_3=\{k_1=v_{123}, k_2=v_{132}=s_2,
k_3=v_{213}=s_1, k_4=v_{231},
k_5=v_{312}, k_6=v_{321}\}, \\
E_3=\{\{v_{123},v_{132}\}, \{v_{123},v_{213}\}, \{v_{132},v_{312}\},
\{v_{213},v_{231}\}, \{v_{231},v_{321}\},\{v_{312},v_{321}\}\}
\end{array}
\end{equation*} 次の等式が成り立ちます。
\begin{equation*}
v_{j_1\cdots j_{i-1}j_ij_{i+1}j_{i+2}\cdots j_n}\circ s_i
=v_{j_1\cdots j_{i-1}j_{i+1}j_ij_{i+2}\cdots j_n}
\end{equation*}($1\leqq i\leqq n-1$であり、
$j_1,j_2,\ldots, j_n$は$1,2,\ldots, n$を並び替えたものです。)
定理B: ([9] 内の定理の一部分) $n\geqq 3$のとき、ケイリーグラフ $(S_n,E_n)$はハミルトン閉路グラフである。
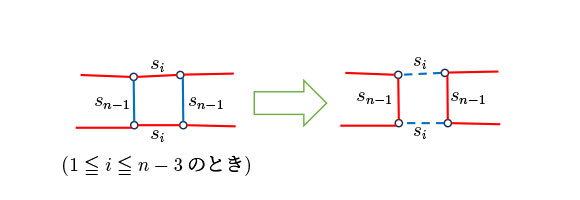
以下の定理Bの証明に用いる厳密な論理は、大学で学ぶ代数学の群論の剰余類という概念を通して理解することが出来ます。ここでは、大まかな説明をします。$n$に関する帰納法を用います。$n=3$のとき$(S_3,E_3)$がハミルトン閉路グラフであるのは明白です。$n\geqq 4$とし、$(S_{n-1},E_{n-1})$はハミルトン閉路グラフであるとします。 $(S_{n-1},E_{n-1})$のハミルトン閉路の上の頂点$v_{j_1\ldots j_{n-1}}\in S_{n-1}$の$j_1\ldots j_{n-1}$の後ろに$n$を加えた$(S_n,E_n)$の頂点$v_{j_1\ldots j_{n-1}n}\in S_n$を対応させることにより $(S_n,E_n)$内の閉路$C_n$を得ます。 さらに各$1\leqq k\leqq n-1$に対して$C_n$の頂点$v_{j_1\ldots k \ldots j_{n-1}n}$の$k$と$n$を入れ替えた頂点$v_{j_1\ldots n \ldots j_{n-1}k}$を対応させることにより新たな閉路$C_k$を得ます。次の等式が定理Bの証明の鍵となるものです。 \begin{equation*} (w\circ s_i)\circ s_{n-1}=(w\circ s_{n-1})\circ s_i \quad (w\in S_n,\,1\leqq i\leqq n-3) \end{equation*} 図4のようにして、$n$個の閉路$C_1,\ldots, C_n$から辺を取り替えることにより次々と閉路をつなげることが出来て、$(S_n,E_n)$のハミルトン閉路を得ることが出来ます。
$n=4$のときは、図5の赤い辺の部分がハミルトン閉路です。
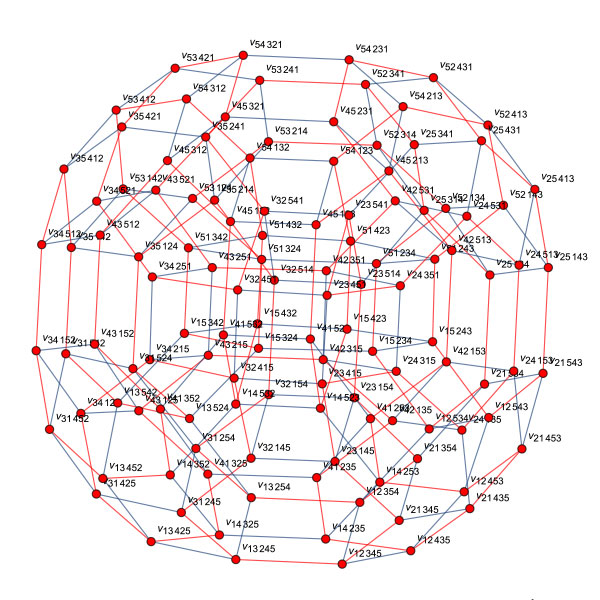
Mathematicaとハミルトン閉路: Mathematica 14.0 $[5]$にはハミルトン閉路を求めるコマンドFindHamiltonianCycleが実装されています。$(S_5,E_5)$のハミルトン閉路はそのコマンドを適用すると瞬時に求まります。
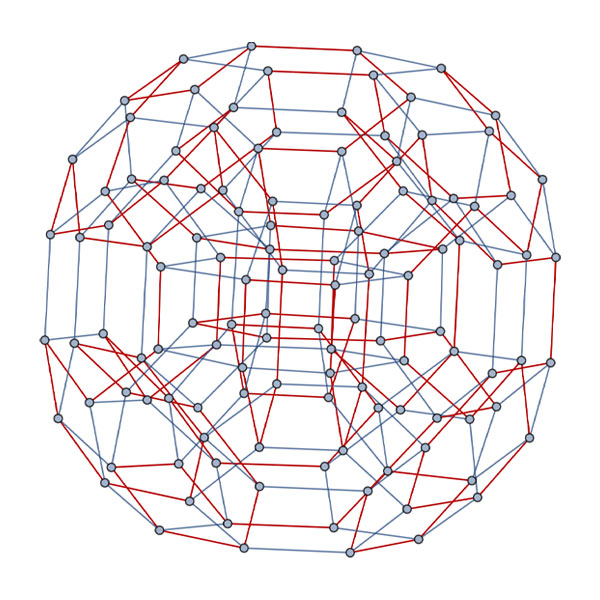
- 図8: Mathematica 14.0 $[5]$のコマンドFindHamltonianCycleにより
- 得られたケイリーグラフ$(S_5,E_5)$のハミルトン閉路
謝辞: 筆者のこの論説に関わる研究は、部分的に、JSPS科学研究費 22K03225 により行われました。また、私が修士課程で研究指導をした井上鷹斗氏との議論が大いに役に立っています。井上鷹斗氏に改めて感謝します。
参考文献
- H. Yamane, Quantized enveloping algebras associated with simple Lie superalgebras and their universal R-matrices, Publ. Res. Inst. Math. Sci. 30 (1994), no. 1, 15-87.
- H. Yamane, On defining relations of affine Lie superalgebras and affine quantized universal enveloping superalgebras, Publ. Res. Inst. Math. Sci. 35 (1999), no. 3, 321-390.
- H. Yamane, Errata to: “On defining relations of affine Lie superalgebras and affine quantized universal enveloping superalgebras”, Publ. Res. Inst. Math. Sci. 37 (2001), no. 4, 615-619.
- I. Heckenberger, H. Yamane, A generalization of Coxeter groups, root systems, and Matsumoto's theorem, Math. Z. 259 (2008), no. 2, 255-276.
- Wolfram Research, Inc., Mathematica 14.0, Wolfram Research, Inc., Champaign, Illinois (2024), https://www.wolfram.com/mathematica/
- H. Yamane, Hamilton circuits of Cayley graphs of Weyl groupoids of generalized quantum groups, Toyama Math. J. 43 (2022), 1-76.
https://toyama.repo.nii.ac.jp/records/20055 - T. Inoue, H. Yamane, Hamiltonian Cycles for Finite Weyl Groupoids, (2023), preprint, arXiv:2310.12543
- E.M. Palmer, The hidden algorithm of Ore's theorem on Hamiltonian cycles, Comput. Math. Appl. 34 (1997), no.11, 113-119.
- J.H. Conway, N.J.A. Sloane, Allan R. Wilks, Gray codes for reflection groups, Graphs and Combinatorics 5 (1989), no. 4, 315-325.
