数理情報学プログラム Program of Mathematics and Informatics

- ホーム
- 数理情報学プログラム
本プログラムは、数学を使って新しい分野を開拓したい人に向いています。サイエンスの分野では数理と情報を融合させた新手法により数多くの発見がされています。また、社会的課題の解決に向けた研究も活発に行われており、数理と情報に対する期待が高まっています。我々と数理と情報の力で新しい世界を切り拓きましょう。
カリキュラム
計算機器やアルゴリズムの発展により、計算不可能と思われていたものが昨今計算可能に変わりつつあります。例えば、観察から得られた画像データを、コンピュータに認識させて人間が行うような認知や判断をさせる研究が数多く報告されています。このようなデータを活用した研究の発展により、サイエンス全体のあり方が変わろうとしています。
本プログラムではこのような最先端の研究を理解するための授業が組まれています。2年次では、数学と情報に関する基本的な内容を学び基礎力を身に付けます。3年次では、理学部DS(データサイエンス)科目や文理融合DS科目を通して、2年次に学んだ内容が、社会科学、自然科学、工学などの分野でどのように活かされるかについて学ぶことができます。また、課題解決型授業を受けることによって実践的な知識を修得することができます。4年次には、それまでに学んだ知識を活かし卒業研究に取り組みます。
研究紹介
コンピュータによる細胞の輪郭抽出アルゴリズム
数学とコンピュータを用いた研究の一例を紹介します。
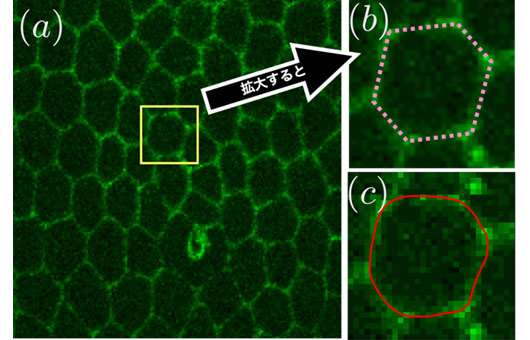
我々のような多くの生物は、細胞を最小単位として成り立っています。右の図(a)はある組織の断面写真で、シャボン泡のような構造がみえると思います。実は泡一つ一つは細胞の輪郭に対応しています (図(b)の点線部分)。この細胞の輪郭を、コンピュータに自動識別させることは可能でしょうか?答えはYesです。図(c)はそのアルゴリズムを構築し、コンピュータで計算させたものですが、赤線のように細胞の輪郭を抽出することができています。これまで、細胞の輪郭の抽出は人間が手作業で膨大な時間をかけて行っていましたが、このような自動アルゴリズムが発展することで大幅に時間の節約をはかることができるようになりました。このような研究の延長には、細胞の輪郭抽出による生物の形づくりの原理解明、異常な形をした細胞による病変の検知等、様々な応用が期待されています。
生物のリズム現象とBZ(ベロウソフ・ジャボチンスキー)反応
心拍の周期、呼吸の周期、睡眠と覚醒の周期など生物には様々なリズムがあります。これらのリズム現象は生物特有のものですが、どのようなメカニズムで生じているのでしょうか?この問に皆さんが高校で実験したような化学反応が肝になっているのではないかと考えた人達がいます。図(a)のシャーレの中では、液にいくつかの化学物質が溶けています。この化学物質のうち、“フェロイン”という物質は還元状態と酸化状態のそれぞれで赤色と青色になることが知られていますが、それが同心円状のパターンとなって観察されます。この化学反応はBZ反応と呼ばれていて、生物のリズム現象を説明する一つの実験モデルとして研究されています。BZ反応は、非常に複雑な反応ですが、その反応のうち大事な変数だけに着目して数理モデルを立てることができます(図下部参照)。この数理モデルをコンピュータシミュレーションしたものが図(b)ですが、実際のBZ反応の特徴を捉えていると思いませんか?この例のように、複雑な現象をそのまま扱うのではなく、より簡単な対象に置き換えて数学的に研究することで、本質が見える場合があります。本プログラムでは、このような数理的考察およびコンピュータシミュレーションの技法を学ぶこともできます。

メッセージ
TOPICS

流れを知る方法と様々な微分方程式
助教 古川 賢
春になると松川など桜の名所を訪れる方が多いかと思う.桜の花びらが川に落ち流れていくが,川の側面に多くの花びらが留まっている様子が観察できる.これはディリクレ境界条件と呼ばれる川をはじめとする流体に課される物理法則に由来する.
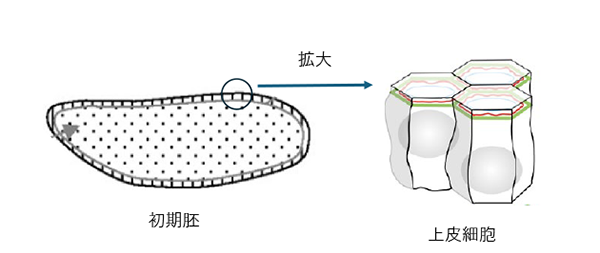
多細胞生物の体づくりの仕組み
特命教授 佐藤 勝彦
私たちを含むすべての多細胞生物は、一つの受精卵から始まって、細胞分裂を繰り返すことによってその体の形が作られていきます(形態形成)。
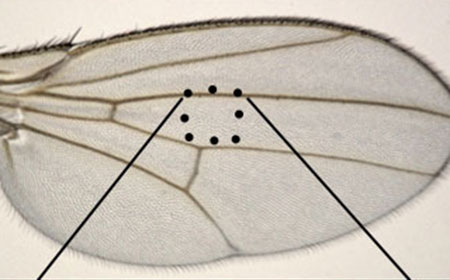
現象解明に数学は使える!
准教授 秋山 正和
2021年11月1日より理学部数学科に着任しました秋山正和と申します.今回は,数学が現象の解明に役立つ可能性を秘めているものであるということをお話させて頂きます.
教員と研究テーマ
自己組織化現象、機械学習、コンピュータシミュレーションなど応用数学に関連した研究をしています。
数学(数理モデル)を用いて、多細胞生物の体のできる仕組み(形態形成)、細胞運動、走性の仕組みを解き明かす研究を行っています。
数学を用いて、生物学、医学、脳科学、物質科学を橋渡しするような融合研究を目指します。
代数体の岩澤理論、有限体上の代数関数体の数論、および計算機数論を研究しています。
応用数学・データ科学.特に位相的データ解析(流線トポロジー解析),数値解析,最適輸送等
計算機と保型形式論を用いた符号理論及び格子理論の数理構造を研究しています。
流体力学に関連する偏微分方程式の性質を調べる研究をしています。

