折り紙の数理

【数学科】川部 達哉

いろいろな形をつくる日本伝統の遊びの一つに「折り紙」があります．近年では折り紙の芸術的側面が再評価され伝承的な折り方以外に新しい折り方も日々考案され続けています．

素材を紙に限定しなければ，我々が生活している社会にも，様々な折りの構造や繰り返される折り模様のパターンがあります．ジャバラ折り，らせん折り，ねじり折り，ミウラ折りなど，折りの特性やデザインを活かした工業製品や造形物は身の回りでも数多く見られます．それだけでなく自然界でも形の特徴をみればそこには必ずと言っていいほど "折り" の構造が入っています．実際，皺や襞も折りの一つと見れば，葉の形，昆虫の羽，地形，タンパク質の折り構造など，上に代表されるような折りに対応するものが各事象において確かに存在し，それぞれの分野においてある種のエネルギー最小問題として現在でも調査･研究されています．

今回はその中で，数学が絡むいくつかのトピックを紹介しましょう．

１．作図問題

平面上でいくつかの点が与えられている時にそこから定規とコンパスを有限回用いて，求めたい点あるいは図形の作図が可能であるか判定することを作図問題といいます．これに関して，古代ギリシャから考えられてきたいくつかの代表的な作図問題の中に次のようなものがあります．

P1:　任意角の三等分線が作図可能か
P2:　正ｎ多角形はすべてのｎについて作図可能か

どちらについても現在は一般には不可能であることが証明されています．
(P.L.Wantzel(1837) によって P1 が，Gauss(1801) によって P2 が示された．)
それらはある有理数係数の既約3次方程式の実数解が与えられた単位の長さをもとに係数に対応する長さから定規とコンパスによって作図できない事に帰結されます．

この定規とコンパスによる作図問題を，今度は折り紙による作図問題として置き換えてみます（ここではそれを折り紙作図ということにします）．それを考えるためには折り紙で可能な作図操作についての自然な公理系をきちんと与えておく必要があります（添付１参照）．

公理系から折り紙作図では，有理数係数の既約3次方程式の実数解がすべて作図できることが示され，これだけでも作図可能性にはより広がりがあることがみてとれます．

具体的には問題 P1 が肯定的に解決されます（添付２参照）．

また問題 P2 についても定規とコンパスによる作図より多くの正多角形を折り紙で作図できます．ただ全ての正n角形が作図できるわけではありません．

一般に定規とコンパスによる作図ではｎが3以上の整数で
n＝2^kp₁p₂p₃ …　（ただしp_i (i=1,2,…) は異なるフェルマー素数（2のべき数uを用いて2^u＋1で表される素数））
と表現できるときに限り作図可能であること，
また，折り紙作図ではｎが3以上の整数で
n＝2^k3^lp₁p₂p₃ … （ただしp_i (i=1,2,…) は2のべき数uやvを指数として表される2^u3^v＋1の形の異なる素数）
と表現できるときに限り作図可能であることが証明されています．これらは作図可能数を考えるときと同様に1 の原始 n 乗根 ζn のガロア群の拡大次数の特徴付けから得られます．いくつか不可能な場合を列挙すると次のようになります．

定規とコンパスによる作図でつくれない正n角形：7,9,11,13,14,18,19,21,22,23,25,26,…，　
折り紙作図でつくれない正n角形：11,22,23,25,29,31,33,41,…．

２．曲面の近似

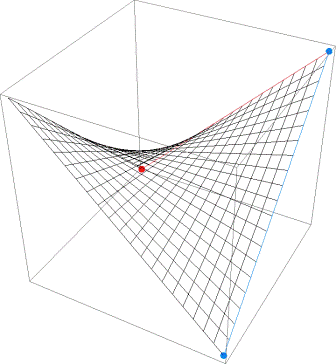
平面に展開できる曲面を可展面といいます．例えば円柱や円錐の側面は可展面です．また直線の連続的な変化からつくられる曲面を線織面といいます．一様双曲面や双曲放物面はその例であるといえます．

可展面は線織面であることは曲面論から示され，もちろん定義より折り紙で表現可能です．しかし線織面の方は一般に可展面であるとは言えないので正確に折り紙で折って表現できるとは一概にいえません（双曲面や放物面は折り紙では正確に表現できない曲面の例です）．ただしジャバラ折りや，らせん折りなどを利用して曲面を近似表現することは可能です（写真参照）．他に，回転面などでも同様な近似方法ができて，こうした技法は曲面の幾何学的モデルの構成方法として利用されます．

一般の曲面についても，折り紙で近似表現する方法が考案されています．

また，逆に擬似曲面として近似した多面体を平坦に折りたたむ方法，さらに一般に曲面近似多面体に限らず種々の多面体について切らずに折り線をつけて平坦に折りたたむ方法なども数多く試案されています．
立体的なものを平坦化したり，平面的なものを立体化する方法と可能性は，実用的な意味でも広く議論されているようです．

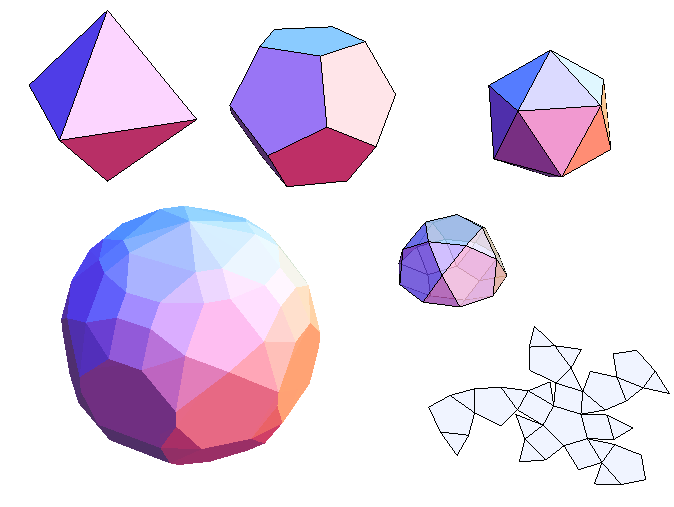
３．多面体とその展開図

ここでは多面体とは単にいくつかの平面に囲まれた立体で，複数の頂点を結ぶ直線の辺と，その辺に囲まれた平坦な多角形によって構成されるものとします．したがって，平坦でない曲面をもつものは含まず，また，すべての面の境界が直線である場合に限られます．
多面体の辺に沿って切り開き，平面に一つながりに重ならずに折り開いたときの図形を展開図といいます．この多面体の展開については（頂点とそれらを結ぶ線で構成された形を考察する）グラフ理論と密接なつながりがあります．
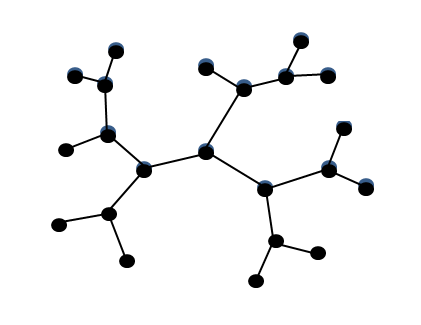
グラフ理論において，閉路のないグラフを木（tree)といい，すべての頂点を通る木のことを全域木（spanning tree）といいます．

また空間の位相不変量のひとつにオイラー標数があります．一般には空間X に対して決まる整数値なのですが，とくにX が多面体の場合，その頂点数をv, 辺の数をe, 面の数をf とおくとき χ(X)＝v－e＋f としてX のオイラー標数χ(X) を定義することができます．
オイラーが多面体の研究においてこの不変量を用いたことからこの名があります．次の定理は様々な曲面や多様体の場合へ拡張されるもので，現今の位相幾何の萌芽的定理の一つといえます，これを利用した「正多面体が５種類しかない」ことを示す証明はとても有名です．

オイラーの多面体定理：　X が球面と同相な多面体ならばχ(X) ＝2である

この多面体定理はグラフ理論を用いて証明できますが，多面体が単連結な（穴のない）展開図をもつ場合は次のように比較的簡単に示すことができます．

（証明の概略）
多面体の面, 辺, 頂点の数をそれぞれ f, e, v とおく．
球面と同相で"単連結な展開図をもつ"ような多面体Xについて (1), (2) がなりたつ．

• (1) 展開するときに切り開く辺（カット辺）と頂点からなるグラフは全域木となる．
  よってその線の個数は v－1 である．
• (2) 展開図の内部領域は単連結なので領域内に現れる辺の個数は f－1 である．

これらより 多面体Xの辺の個数を考えるとe＝(v－1)+(f－1) となり，
これは χ(X)＝v－e＋f＝2 であることを意味している．■

一般に多面体は常に展開図をもつわけではなく，実は展開図をもたない多面体も存在します．それでも任意の凸多面体なら，いつでも展開図をもつことは正しく平易に示されるように思えます．しかしこれは現時点では部分的にしか解決していない未解決問題です．

さらに辺以外の任意の場所を切ることを許した展開を一般展開といいますが，一般展開による展開図には意外な形が数多くあります．ここに添付された展開図（添付３参照）からさまざまな四面体を折ってみるとその不思議な一般展開の一端に触れることができます．

• ・与えられた多角形からどんな凸多面体が折れるのか？
• ・どんな多面体でも一般展開できるのか？
• ・凸多面体を折れる多角形の形に関する特徴づけはあるのか？

など一般展開においても未解決な問題が数多く残されているようです．

【参考文献】

1. Geometric Folding Algorithms: Linkages, Origami, Polyhedra
   Erik D. Demaine and Joseph O'Rourke.
   Cambridge University Press, July 2007.
   ISBN 978-0-521-85757-4.