循環小数の一性質 －Midy の定理とその一般化－

【数学科】濱名 正道

　有理数1/7 は, 10 進法では, 次のように循環小数で表されます:

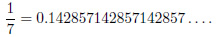
この右辺で周期的に繰り返して現れる142857 の形の数の列を循環節と呼びますが, この循環節を142, 857あるいは14, 28, 57 のように分割して加えると次のようになります:

142 + 857 = 999,　　　(1)
14 + 28 + 57 = 99.　　(2)

つまり, 数字の列142857 を同数ずつそれぞれ2 個142, 857 及び3 個14, 28, 57 に分割し, 加えたものが9 をいくつか並べた数になります. ここで, 足し算は, 上記の数の列を10 進法で表示された自然数と見なして行っています.

　1/7 以外の, いくつかの有理数の小数展開についても調べてみます. 尚, 以下では, 循環節をbar ￣を用いて,

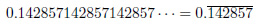
のように表すことにします.

　これらの性質は, もっと一般の有理数の小数表示について成り立つ性質です. 1/p (p は素数) が, (1) の形の性質をもつこと, 即ち,

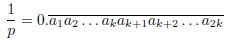
のように循環節の長さが偶数のとき, 循環節 a₁a₂ . . . a_ka_k+1a_k+2 . . . a_2k を

a₁a₂ . . . a_k, a_k+1a_k+2 . . . a_2k

と二つに分割するならば,

a₁ + a_k+1 = 9, a₂ + a_k+2 = 9, . . . , a_k + a_2k = 9　　　(3)

であることは, 古くから知られている結果で, Midy の定理(Midy 1836) と呼ばれます. しかし, (2) の形の性質(長さが3 の倍数である循環節を3 個に分割する場合, あるいは, もっと一般に, 長さがd 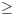2 の倍数である循環節をd 個に分割する場合) が, ある程度一般の有理数に対して成り立つことが示されたのは, 比較的最近で, 2004 年のGinsberg の論文(Ginsberg 2004) の発表以降です. ここでは, このような循環小数の性質を, 主に, Lewittes 2007 に従って紹介します.

※続きは、下記リンクのPDFよりご覧ください。
• 循環小数の一性質 －Midy の定理とその一般化－（PDF 130KB）