複雑な振る舞いを生み出す漸化式

【数学科】上田 肇一

次の漸化式はある生物種の個体数の時間変化を記述する数理モデルです。

x(n+1) = a×x(n)×(1-x(n)), x(0)=0.1 (1)

ここで、x(n)は時刻（年）nにおけるある生物種の個体数、aは個体数の増加率に関わる定数です。この方程式の見た目は非常に単純なため、解（一般項）を手計算で求めることができるのでは？と思われるかもしれませんが、残念ながら特別な場合を除き、解を書き下すことは困難です。そこで、ここでは漸化式を解くことは諦めて、計算機を用いて個体数の時間変化を調べてみます。

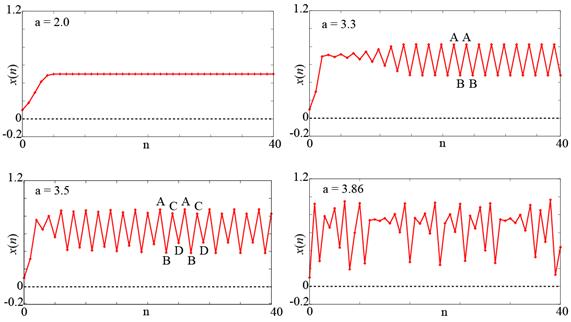
例えばa=2としてみましょう。x(0)=0.1ですからx(1)=2×0.1×(1-0.1)=0.18となります。x(2)の値はx(1)を式(1)の右辺に代入することで得ることができ、計算機を用いてx(n)を計算すると図1のような結果が得られます。a=2の場合はx(n)（生物の個体数）はある一定の値に近づきます（生物の個体数が一定になるということは安定な状態といえるでしょう）。

さて、aの値をもう少し大きくしてみます。例えばa=3.3としてみると、一定な状態に落ち着かずに2つの状態をABABのように繰り返す周期的振動が観察されます（図1 a=3.3）。さらにaを大きくしてa=3.5とするとABCDABCDのように4つの状態を繰り返す周期的振動が見られます（図1 a=3.5）。さらに大きくすると今度は8つの状態を繰り返し、さらに注意深くaの値を大きくしていくと16状態、32状態と2の倍数で周期が増加していきます（個体数が毎年振動する不安定な状態です）。このような変化は周期倍分岐と呼ばれます。この周期倍分岐はあるaの値（3.6付近）で終了し、図1(a=3.86)のように複雑な現象が現れ始めます。このような複雑な振る舞いは「カオス」と呼ばれています（来年の個体数は予想が困難な状態になります）。ちなみに、aを4.0未満の範囲で増加させると周期的振動と複雑な振る舞いが繰り返し現れることが知られています。

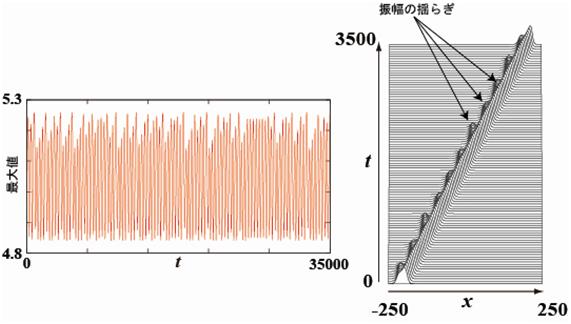
式(1)はロジスティック方程式と呼ばれており、多くの研究者によって解析が行われ、カオスの発生機構が解明されました。このような単純な方程式を解析することに意味があるのか？また、世の中の役に立つことがあるのか？という疑問が湧くかもしれません。しかし、この研究をきっかけとして物理学、生物学、工学において数多くのカオスが発見されました。我々はある化学反応に現れるパルスの振幅が周期倍分岐の後にカオス的になることを数値実験によって発見しました[1]（図2）。また、カオスの工学的応用が期待されており、当研究室でも経路探索アルゴリズムにカオスを応用する試みを行っています。

【参考文献】

1. Yadome, Masaaki, Kei-Ichi Ueda, and Masaharu Nagayama. "Chaotic motion of propagating pulses in the Gray-Scott model." Physical Review E 83.5 (2011): 056207.