数学科 Mathematics

- ホーム
- 数学科
数学科高度に抽象化された現代数学は、さらなる抽象化と同時に私たちの身近に新しい題材を求めています。数学科では数理解析と情報数理の2大分野によってこの動向に思い切った対処の仕方をしています。数理解析分野では純粋数学の立場からきめ細かな教育・研究を行い、情報数理分野では時代のニーズに応えて情報科学に関する教育・研究を数学の立場から行っています。数学科で私たちと一緒に学んでみませんか?
カリキュラム
数学科のカリキュラムの特徴は、なにより数学をきちんと学ぶこと、そして、情報関連科目の充実にあります。また、数学・自然科学に関する英語教育にも力を注いでいます。 1年次では、教養教育の各科目の履修が中心となります。更に、専門教育科目として、大学での数学教育の中核をなす「解析学」と「線形代数学」を学びます。これらの科目に対しては、論理的に考える力と計算する力を同時に養うための授業が展開されていて、数学の基礎を身につけることができます。また、「数学序論」では、高校から大学への橋渡しを意図として大学で数学を学んでいくのに必要な知識、技術を習得します。たとえば高校の数学の授業では使われることのなかった表現や記号、そして集合や写像、初歩的な論理学などです。2年次以降は、専門教育科目が開講されます。2年次には、1年次の内容を踏まえてより発展した内容を学び、3年次には高度な現代数学の研究に向けた授業が展開されます。4年次では、それまでに学んだ数学の総仕上げとして、「卒業研究」を行います。数学の専門書を英語で読む技術、理解したことを論理的に伝える技術、議論する技術を身につけながら研究を進めていきます。 数学科では、豊富な純粋数学の授業に加え、情報関連科目を充実させています。1年次では、教養教育の「情報処理」があり、大学生活は勿論、社会に出てからも有益なITリテラシーを身につけます。2年次以降、情報科学関連科目が理論・実習ともに開講され、3、4年次での専門的な講義に発展していきます。 英語教育についても、教養教育の英語の授業の他、3年次では、自然科学の様々な話題に英語で親しむ「科学英語」の授業があり、4年次の卒業研究にスムーズに移行できるようになっています。
分野紹介
【数理解析分野】Mathematical Analysis
数理解析分野では、幾何学、代数学、解析学などを中心に純粋数学の立場から教育・研究を行っています。ここでの教育目標は、学生に純粋数学の世界の一端に触れ、抽象数学の美しさを味わい、厳密な理論の構成の仕方を身につけてもらうことです。
数理解析分野では次のような研究が行われています。
- 空間図形の性質、曲線や曲面の概念を一般化した多様体などを調べる幾何学(抽象的幾何学構造を見る数学的直観力の強化にコンピュータは役立つか?)
- 複素関数(複素数に対して複素数を対応させる関数)の性質を調べる複素関数論(華麗な姿を見せるフラクタルもこの理論に属しています)。
- 数の概念を拡張して種々の視点から数の性質を調べる数論(ネット間での情報のやり取りを保証する暗号・認証にも使われます)。
- 足し算や掛け算などの演算の性質を調べる代数学(歴史の古いこの分野の理論には美しさがあります)。


【情報数理分野】Mathematical Science of Information
この分野は、数理現象の数学的解析とその手法の開拓という視点を持つ教員によって構成されています。コンピュータ等を用い、数学的手法を駆使して数理現象を解析する能力を習得することがこの分野の教育目標です。
情報数理分野では、次のような研究が行われています。
- 微分方程式の解の性質を研究する微分方程式論(微分方程式はさまざまな現象を記述する数学の言語です)。
- 数理現象のモデル化とモデル方程式の数学的・数値的解析(現状では数値的にしか解けない複雑な現象も扱います)。
- 偶然性に支配される現象を解析する確率論(近年のファイナンス理論の進展に確率論は大きく寄与しています)。
- コンピュータを使った「群」「環」「体」などの代数系の構造を調べる研究(とくに量子代数と呼ばれる近年に発見された新しい代数系の研究をコンピュータによるグレブナー法で解析します)。


学生メッセージ
TOPICS
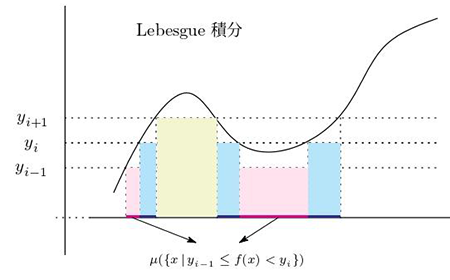
積分を特徴付ける3つの性質
‐測度を定める汎関数‐
教授 菊池 万里
「(定)積分」と聞いて先ず(というより唯一)思い浮かぶのは、高校で学習した\[ \int_a^b f(x)\,dx \]という形の積分だと思います。
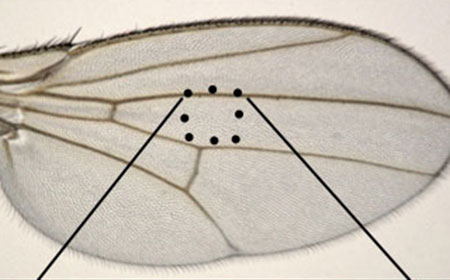
現象解明に数学は使える!
准教授 秋山 正和
2021年11月1日より理学部数学科に着任しました秋山正和と申します.今回は,数学が現象の解明に役立つ可能性を秘めているものであるということをお話させて頂きます.

ガロア理論について
教授 山根 宏之
最初は筆者の研究を紹介しようとしたが,非専門家向けに数学的な概念を説明するのは困難である事に気が付いた.
教員と研究テーマ
自己組織化現象、機械学習、コンピュータシミュレーションなど応用数学に関連した研究をしています。
Lorentz空間などに代表される再配列不変空間におけるマルチンゲールの理論を研究しています。
多様体上の幾何学、特に等質空間などを研究しています。
空間の中に、どのような曲面がどのように入っているかを微分積分学を用いて調べる、部分多様体論という分野の研究をしています。
解析汎関数論、解析関数の積分公式とその応用について研究しています。
Hamilton-Jacobi方程式と病的函数の間の対応構造について研究しています。
スーパーリー代数や量子群をコクセター半群の理論を整備しながら研究しています。
数学を用いて、生物学、医学、脳科学、物質科学を橋渡しするような融合研究を目指します。
多様体への不連続な群作用や、それらの空間形の幾何学について研究しています。
代数体の岩澤理論、有限体上の代数関数体の数論、および計算機数論を研究しています。
コロンボの一般関数の理論を用いた偏微分方程式の研究を行っています。
計算機と保型形式論を用いた符号理論及び格子理論の数理構造を研究しています。



